In matematica, la geometria del taxi o distanza di Manhattan (Taxicab geometry oppure Manhattan distance in inglese), studiata da Hermann Minkowski nel XIX secolo, è un tipo di geometria in cui la metrica usuale della geometria euclidea è stata sostituita da una nuova metrica in cui la distanza tra due punti è la somma delle differenze (in valore assoluto) delle loro coordinate.
Indice
-
1 Distanza nella geometria del taxi
2 Scacchi
3 Voci correlate
4 Collegamenti esterni
Distanza nella geometria del taxi
Formalmente, si può definire la distanza nella geometria del taxi (in inglese Manhattan distance), indicata come distanza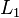 
, tra due punti nello spazio euclideo con un fissato sistema di coordinate cartesiane, la somma delle lunghezze delle proiezioni sugli assi cartesiani dei segmenti che congiungono i due punti.
Per esempio, nel piano, la distanza 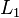tra due punti 
di coordinate 
e il punto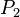 
di coordinate 
è
Si noti che la distanza 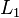varia se il sistema di assi cartesiani ruota, mentre è invariante per traslazioni degli assi o per riflessioni rispetto ad un asse coordinato.
La distanza 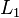viene anche detta distanza del taxi, perché è la minore distanza che dovrebbe essere percorsa da un’automobile per muoversi tra due punti situati in una città suddivisa in isolati quadrati, come Manhattan o Torino (tralasciando naturalmente i sensi unici e le eventuali strade oblique, e anche il fatto che nelle città le strade esistono solo ai bordi degli isolati, non esiste la 3.14-esima strada). Ogni percorso che va da un punto a un altro punto situato 3 isolati a est e 6 isolati a nord dovrà essere lungo almeno 9 isolati. Tutte le strade più dirette sono lunghe esattamente 9 isolati.
Rispetto alla geometria euclidea, nella geometria del taxi non vale il primo criterio di congruenza dei triangoli: è possibile generare due triangoli diversi aventi due lati e l’angolo fra essi compreso ordinamente congruenti. Rimane valido, invece, il postulato delle parallele.
Una circonferenza nella geometria del taxi è il luogo di punti che hanno la stessa distanza 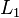dal centro. Queste circonferenze sono in realtà quadrati i cui lati formano un angolo di 45° con gli assi coordinati. In questo contesto, il rapporto fra la lunghezza di una circonferenza ed il raggio 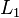non è 
, bensì 8.
Scacchi
Nel gioco degli scacchi, la distanza tra le caselle sulla scacchiera per una torre viene misurata secondo la distanza della geometria del taxi. Il re e la regina usano invece la distanza di Chebyshev, e l’alfiere usa invece la distanza della geometria del taxi (tra caselle dello stesso colore) sulla scacchiera ruotata di 45 gradi, cioè con le diagonali coincidenti con gli assi cartesiani. Per spostarsi da una casella a un’altra, solo i re hanno bisogno di un numero di mosse uguali alla distanza; torri, regine e alfieri hanno bisogno invece di una o due mosse (su una scacchiera vuota e assumendo, per l’alfiere, che la mossa sia possibile).
tratto da: it.wikipedia.org/wiki/Geometria_del_taxi
Questi sono i compitini per le vacanze. A Settembre facciamo le interrogazioni 😉
se fossi cosi’ “studiato” giocherei a poker professionale!
In realtà è molto piu semplice di quello che sembra..
dice semplicemente che in uno spazio diviso in segmenti lineari e non diagonali (solo verticale e orizzontale) la distanza fra 2 punti si calcola con in numero di segmenti che devi attraversare , e che quindi fra 2 percorsi quello piu corto è quello con meno segmenti.. (mava’ ! :)), detto in parole diverse se non ci sono ostacoli nel percorso il numero minimo dei segmenti è uguale alla differenza delle coordinate dei 2 punti (arrivo e partenza) in valore assoluto..